- Autor Jason Gerald [email protected].
- Public 2024-02-01 14:15.
- E modifikuara e fundit 2025-01-23 12:47.
Të gjithë mund të mësojnë Matematikë nëse janë tashmë në një fazë më të lartë në shkollë ose thjesht duan të përmirësojnë bazat përsëri. Pasi të keni diskutuar se si të jeni një nxënës i mirë në Matematikë, ky artikull do t'ju mësojë përparimet themelore të matematikës dhe do t'ju japë elementët bazë që do t'ju duhet të mësoni në secilën praktikë. Pastaj, ky artikull do të diskutojë bazat e mësimit të aritmetikës, i cili do të ndihmojë si fëmijët e shkollës fillore ashtu edhe këdo që dëshiron të mësojë bazat e kësaj fushe të shkencës.
Hapi
Pjesa 1 nga 6: Çelësat për t'u bërë një student i mirë i matematikës

Hapi 1. Paraqiteni në klasë
Kur humbisni orën e mësimit, duhet të mësoni koncepte nga shokët e klasës ose nga libri juaj shkollor. Ju kurrë nuk do të merrni një përmbledhje teksti nga një mik sa më shumë që merrni nga mësuesi juaj.
- Ejani në klasë në kohë. Në vend të kësaj, mbërrini pak herët dhe hapni fletoren tuaj në vendin e duhur, hapni librin tuaj shkollor dhe nxirrni kalkulatorin tuaj në mënyrë që të jeni gati të filloni kur mësuesi juaj të jetë gati për të dhënë mësim.
- I pafuqishëm vetëm nëse jeni i sëmurë. Nëse me të vërtetë ju mungon mësimi, pyesni shokët tuaj të klasës që të zbulojnë për çfarë po fliste mësuesi dhe çfarë detyrash iu dhanë.

Hapi 2. Punoni me mësuesin tuaj
Nëse mësuesi juaj po punon për një problem para klasës, punoni me mësuesin duke punuar në problemin në fletoren tuaj.
- Sigurohuni që shënimet tuaja të jenë të qarta dhe të lehta për tu lexuar. Mos shkruani vetëm pyetje. Gjithashtu shkruani çdo gjë që thotë mësuesi që mund të përmirësojë të kuptuarit tuaj për konceptet që shpjegohen.
- Plotësoni pyetjet e dhëna nga mësuesi juaj. Ndërsa mësuesi ecën nëpër klasë ndërsa punoni, përgjigjuni pyetjeve që bëhen.
- Merrni pjesë kur mësuesi zgjidh një problem. Mos prisni që mësuesi t'ju thërrasë. Ofroni përgjigje kur e dini përgjigjen dhe ngrini dorën për të bërë një pyetje nëse nuk jeni të sigurt për materialin që mësohet.

Hapi 3. Bëni detyrat e shtëpisë tuaj në të njëjtën ditë kur jepen detyrat e shtëpisë
Nëse i bëni detyrat e shtëpisë në të njëjtën ditë, koncepti është ende i freskët në mendjen tuaj. Ndonjëherë, përfundimi i detyrave të shtëpisë tuaj në të njëjtën ditë nuk është i mundur. Sigurohuni që detyrat e shtëpisë janë bërë para se të shkoni në klasë.

Hapi 4. Punoni jashtë klasës nëse keni nevojë për ndihmë
Vizitoni mësuesin tuaj gjatë pushimeve ose gjatë orarit të punës.
- Nëse keni një Qendër Matematike në shkollën tuaj, mësoni orët e saj të punës dhe kërkoni ndihmë.
- Bashkohuni në një grup studimi. Një grup i mirë studimi në përgjithësi përbëhet nga 4 ose 5 persona me nivele të ndryshme aftësish. Nëse jeni student "C" në Matematikë, bashkohuni me një grup prej 2 ose 3 studentësh me nota "A" ose "B", në mënyrë që të përmirësoni aftësitë tuaja. Shmangni bashkimin me një grup studentësh, notat e të cilëve janë më të ulëta se tuajat.
Pjesa 2 nga 6: Mësimi i matematikës në shkollë

Hapi 1. Filloni me aritmetikë
Në shumicën e shkollave, nxënësit mësojnë aritmetikë në shkollën fillore. Aritmetika mbulon bazat e mbledhjes, zbritjes, shumëzimit dhe pjesëtimit.
- Bëni pyetje praktike. Bërja e problemeve aritmetike pa pushim është mënyra më e mirë për të mësuar përmendësh bazat në mënyrë korrekte. Shikoni për softuer që mund t'ju japë një larmi problemesh të ndryshme të Matematikës për të punuar. Gjithashtu, kërkoni probleme me afatet kohore për të përmirësuar shpejtësinë tuaj.
- Ju gjithashtu mund të gjeni probleme aritmetike në internet dhe mund të shkarkoni aplikacione aritmetike në pajisjen tuaj celular.

Hapi 2. Vazhdoni me para-algjebrën
Ky ushtrim do t'ju ofrojë elementet bazë që do t'ju nevojiten për të zgjidhur problemet e algjebrës më vonë.
- Mësoni rreth thyesave dhe dhjetoreve. Do të mësoni të shtoni, zbritni, shumëzoni dhe ndani thyesa dhe dhjetore. Lidhur me thyesat, do të mësoni se si të zbritni thyesat dhe të përktheni numrat e kombinuar. Sa i përket numrave dhjetorë, ju do të kuptoni vlerat e vendeve dhe do të jeni në gjendje të përdorni decimale në problemet e historisë.
- Mësoni rreth raporteve, proporcioneve dhe përqindjeve. Këto koncepte do t'ju ndihmojnë të mësoni të bëni krahasime.
- Prezantoni veten në gjeometrinë bazë. Do të mësoni forma dhe koncepte 3D. Ju gjithashtu do të mësoni koncepte si zona, perimetri, vëllimi dhe sipërfaqja, si dhe informacion në lidhje me linjat dhe këndet paralele dhe pingul.
- Kuptoni disa statistika bazë. Në para-algjebër, futja juaj në statistika në përgjithësi përfshin pamje të tilla si grafikët, tabelat e shpërndarjes, tabelat e komplotit të pullave dhe histogramet.
- Mësoni bazat e algjebrës. Kjo përfshin koncepte të tilla si zgjidhja e ekuacioneve të thjeshta që përmbajnë variabla, mësimi i vetive të tilla si vetia shpërndarëse, vizatimi i ekuacioneve të thjeshta dhe zgjidhja e pabarazive.
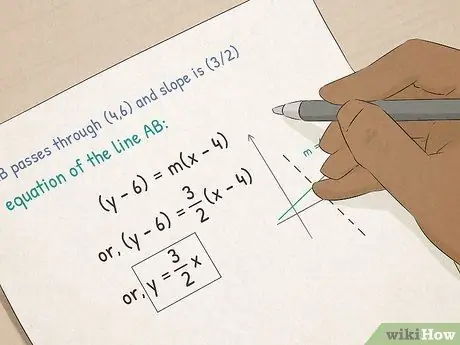
Hapi 3. Përparimi në Algjebër I
Në vitin tuaj të parë të algjebrës, do të mësoni për simbolet bazë të përfshira në algjebër. Ju gjithashtu do të mësoni të:
- Të zgjidhin ekuacionet dhe pabarazitë që përmbajnë ndryshore. Ju do të mësoni se si t'i zgjidhni këto probleme në letër dhe si t'i zgjidhni ato me fotografi.
- Zgjidh problemet e historisë. Do të habiteni se sa probleme të përditshme do të hasni në të ardhmen që kërkojnë aftësinë për të zgjidhur problemet e historisë algjebrike. Për shembull, ju do të përdorni algjebër për të gjetur normën e interesit që fitoni në llogarinë ose investimin tuaj bankar. Ju gjithashtu mund të përdorni algjebër për të kuptuar se sa gjatë duhet të udhëtoni bazuar në shpejtësinë e makinës tuaj.
- Punoni me eksponentë. Kur filloni të zgjidhni ekuacionet polinomiale (shprehje që përmbajnë numra dhe ndryshore), do të kuptoni se si të përdorni eksponentët. Kjo ndoshta do të përfshijë ushtrime me shënim shkencor. Pasi të zotëroni eksponentët, mund të mësoni të shtoni, zbritni, shumëzoni dhe ndani shprehje polinomiale.
- Zgjidh problemet e katrorit dhe rrënjës katrore. Ndërsa zotëroni këtë temë, do të jeni në gjendje të mësoni përmendësh katrorët e shumë numrave. Ju gjithashtu do të jeni në gjendje të punoni me ekuacione që kanë rrënjë katrore.
- Kuptoni funksionet dhe grafikët. Në algjebër, do të mësoni rreth ekuacioneve grafike. Ju do të mësoni se si të llogarisni pjerrësinë e një drejtëz, si të vendosni një ekuacion në formën e pjerrësisë pikë dhe si të llogaritni fetë x-dhe-y të një linje duke përdorur formën e përgjimit të pjerrësisë.
- Gjeni sistemin e ekuacioneve. Ndonjëherë, ju jepen 2 ekuacione të ndryshme me ndryshoret x dhe y, dhe ju duhet të zgjidhni për x ose y për të dy ekuacionet. Për fat të mirë, do të mësoni shumë truke për zgjidhjen e këtyre ekuacioneve, përfshirë grafikimin, zëvendësimin dhe shtimin.

Hapi 4. Studioni gjeometrinë
Në gjeometri, do të mësoni për vetitë e vijave, segmenteve, këndeve dhe formave.
- Ju do të mësoni përmendësh një numër teoremash dhe përfundimesh që do t'ju ndihmojnë të kuptoni rregullat e gjeometrisë.
- Do të mësoni se si të llogarisni sipërfaqen e një rrethi, si të përdorni teoremën e Pitagorës dhe si të gjeni marrëdhënien midis këndeve dhe anëve të një trekëndëshi të veçantë.
- Ju do të shihni shumë pyetje gjeometrike në testet e standardizuara të ardhshme të tilla si SAT, ACT dhe GRE.
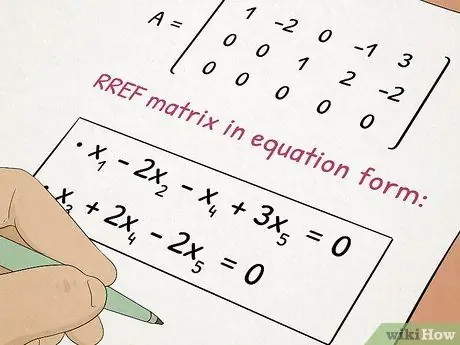
Hapi 5. Merrni klasën e Algjebrës II
Algjebra II bazohet në konceptet që keni mësuar në Algjebër I ndërsa shtoni tema komplekse siç janë ekuacionet dhe matricat kuadratike.
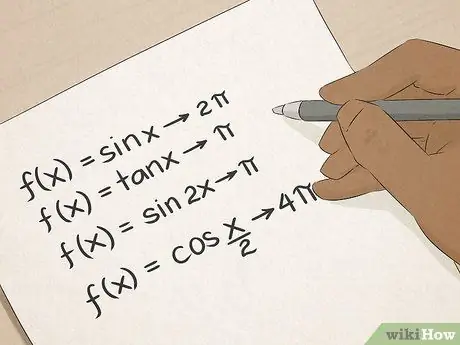
Hapi 6. Zotëroni trigonometrinë
Ju i njihni termat trigonometrikë: sinus, kosinus, tangjent, etj. Trigonometria do t'ju mësojë shumë mënyra praktike për të llogaritur këndet dhe gjatësinë e linjave, dhe këto aftësi do të jenë të paçmueshme për njerëzit që punojnë në ndërtim, arkitekturë, inxhinieri ose rilevim.
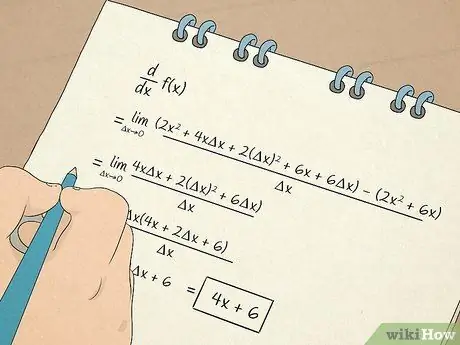
Hapi 7. Kryeni llogaritjet e llogaritjes
Llogaritja mund të tingëllojë frikësuese, por është një mjet i mrekullueshëm për të kuptuar ose sjelljen e numrave ose botën përreth jush.
- Llogaritja do t'ju mësojë funksionet dhe kufijtë. Ju do të shihni sjelljen e numrit të funksioneve të dobishme duke përfshirë e^x dhe funksionet logaritmike.
- Ju gjithashtu do të mësoni se si të llogaritni dhe punoni me derivatet. Derivati i parë ju jep informacion bazuar në pjerrësinë e vijës tangjente në një ekuacion. Për shembull, një derivat ju tregon shkallën me të cilën diçka ndryshon në një situatë jo-lineare. Derivati i dytë do t'ju tregojë nëse funksioni rritet ose zvogëlohet gjatë një intervali të caktuar, kështu që ju mund të përcaktoni konkavitetin e një funksioni.
- Integralët do t'ju mësojnë se si të llogaritni sipërfaqen nën një kurbë, si dhe vëllimin e saj.
- Llogaritja në shkollën e mesme në përgjithësi përfundon në sekuenca dhe sekuenca. Edhe pse studentët nuk do të shohin shumë aplikime për qarqet, qarqet janë të rëndësishme për ata që studiojnë ekuacionet diferenciale.
Pjesa 3 nga 6: Bazat e Matematikës-Shtesa Master

Hapi 1. Filloni me faktet "+1"
Shtimi i 1 në një numër ju çon në numrin më të lartë në rreshtin e numrave. Për shembull, 2 + 1 = 3.
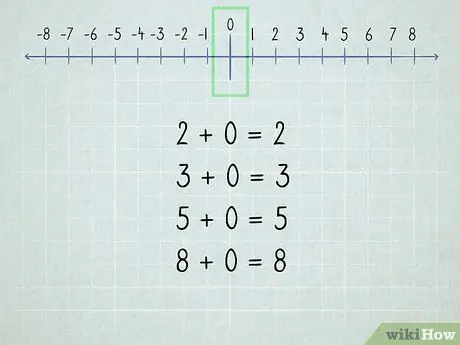
Hapi 2. Kuptoni zero
Të gjithë numrat e shtuar në zero janë i njëjti numër sepse "zero" do të thotë "asnjë".

Hapi 3. Mësoni numra të dyfishtë
Numrat e shumtë janë një problem që përfshin shtimin e dy numrave të barabartë. Për shembull, 3 + 3 = 6 është një shembull i një ekuacioni që përfshin numra të shumtë.

Hapi 4. Përdorni hartëzimin për të mësuar rreth zgjidhjeve të tjera shtesë
Në shembullin e mëposhtëm, ju mësoni duke shënuar se çfarë ndodh kur shtoni 3 në 5, 2 dhe 1. Provoni vetë problemin "shto me 2".

Hapi 5. Vazhdoni derisa numri të jetë më shumë se 10
Mësoni të mbledhni 3 numra së bashku për të marrë një numër më të madh se 10.
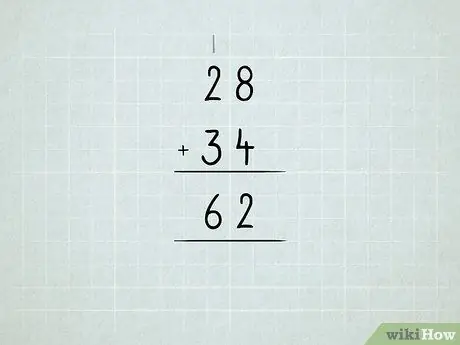
Hapi 6. Shtoni numrat më të mëdhenj
Mësoni rreth grupimit të njësive në dhjetëra, dhjetëra në qindra, e kështu me radhë.
- Shtoni së pari numrat në kolonën e djathtë. 8 + 4 = 12, që do të thotë se keni 1 numër 10 dhe 2 numër 1. Shkruani numrin 2 nën kolonën e njësive.
-
Shkruani numrin 1 në kolonën dhjetëshe.
-
Shtoni kolonën dhjetëra në tërësinë e saj.
Pjesa 4 nga 6: Bazat matematikore-Strategjitë e reduktimit

Hapi 1. Filloni me "1 shifër prapa
Zbritja e 1 nga një numër ju merr mbrapa 1 numër. Për shembull, 4 - 1 = 3.

Hapi 2. Mësoni të zbritni numra të dyfishtë
Për shembull, ju shtoni numrat 5 + 5 për të marrë 10. Thjesht shkruani ekuacionin mbrapsht për të marrë 10 - 5 = 5.
- Nëse 5 + 5 = 10, atëherë 10 - 5 = 5.
-
Nëse 2 + 2 = 4, atëherë 4 - 2 = 2.

Hapi 3. Mësoni përmendësh familjen e fakteve
Si nje shembull:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Hapi 4. Gjeni numrat që mungojnë
Për shembull, _ + 1 = 6 (përgjigja është 5).

Hapi 5. Mësoni përmendsh faktin e zbritjes në 20

Hapi 6. Praktikoni zbritjen e numrave 1-shifrorë nga numrat 2-shifrorë pa marrë hua
Zbritni numrat në kolonën njëshe dhe zvogëloni numrat në kolonën dhjetëra.
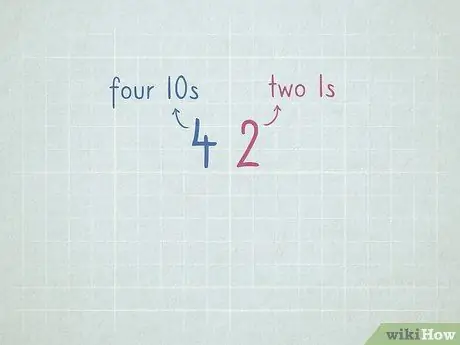
Hapi 7. Praktikoni vlerën e vendit për t'u përgatitur për zbritjen me huamarrje
- 32 = 3 numra 10 dhe 2 numra 1.
- 64 = 6 numra 10 dhe 4 numra 1.
- 96 = _ numri 10 dhe _ numri 1.
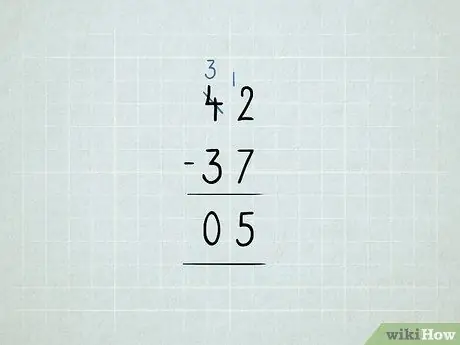
Hapi 8. Zbrit me huamarrje
- Ju dëshironi të zbritni 42 - 37. Filloni duke u përpjekur të zbritni 2 - 7 në kolonën e njësive. Doli, nuk funksionoi!
-
Huazoni numrin 10 nga kolona dhjetëshe dhe vendoseni në kolonën njëshe. Tani keni 3 10 në vend të 4 10. Tani keni 12 1 në vend të 2 1.
-
Zbritni së pari kolonën e njësive tuaja: 12 - 7 = 5. Pastaj, kontrolloni kolonën dhjetëshe. Meqenëse 3 - 3 = 0, nuk keni nevojë të shkruani numrin 0. Përgjigja juaj është 5.
Pjesa 5 nga 6: Bazat e Matematikës-Shumëzimi Master

Hapi 1. Filloni me numrin 1 dhe numrin 0
Të gjithë numrat që shumëzohen me 1 janë të njëjtë me vetë numrin. Çdo numër i shumëzuar me 0 është i barabartë me zero.

Hapi 2. Mësoni përmendësh tabelën e shumëzimit

Hapi 3. Praktikoni me probleme të shumëzimit një shifror

Hapi 4. Shumëzoni numrin 2 shifror me numrin 1 shifror
- Shumëzoni numrin e poshtëm të djathtë me numrin e sipërm të djathtë.
-
Shumëzoni numrin e poshtëm të djathtë me numrin e sipërm të majtë.
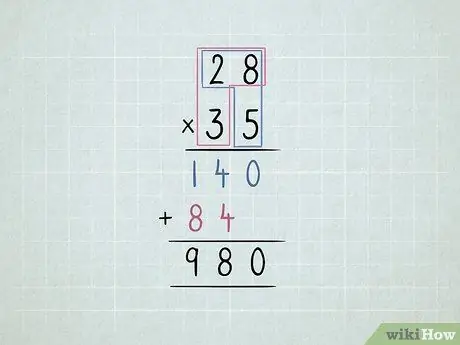
Hapi 5. Shumëzoni 2 numra 2-shifrorë
- Shumëzoni numrin e poshtëm të djathtë me numrin e sipërm të djathtë dhe pastaj me numrin e sipërm të majtë.
-
Zhvendosni rreshtin e dytë një shifër në të majtë.
- Shumëzoni numrin e poshtëm të majtë me numrin e sipërm të djathtë dhe pastaj numrin e sipërm të majtë.
-
Shtoni të gjitha kolonat.
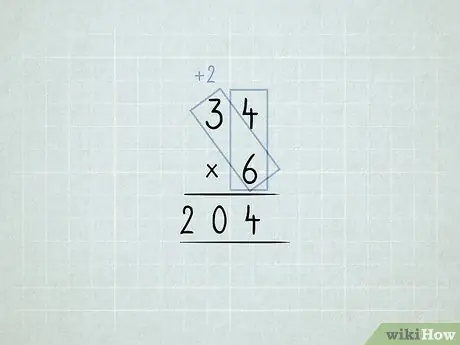
Hapi 6. Shumëzoni dhe rigruponi kolonat
- Ju dëshironi të shumëzoni 34 x 6. Filloni duke shumëzuar kolonën e njësive (4 x 6), por nuk mund të keni 24 1s në kolonën njësi.
-
Ruani 4 1 në kolonën e njësive. Lëvizni 2 10 në kolonën dhjetëshe.
-
Shumëzoni 6 x 3, e barabartë me 18. Shtoni 2 -ën që keni lëvizur, e cila është e barabartë me 20.
Pjesa 6 nga 6: Bazat matematikore-Zbuloni probleme të ndarjes

Hapi 1. Mendoni për ndarjen në krahasim me shumëzimin
#* Nëse 4 x 4 = 16, atëherë 16 /4 = 4.
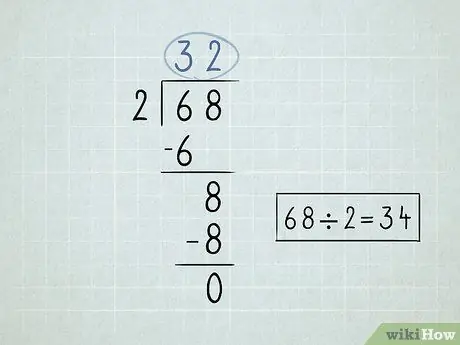
Hapi 2. Shkruani problemin tuaj të ndarjes
- Ndani numrin në të majtë të simbolit të pjesëtimit, ose pjesëtuesit, me numrin e parë nën simbolin e pjesëtuesit. Meqenëse 6/2 = 3, ju do të shkruani numrin 3 mbi simbolin e pjesëtimit.
-
Shumëzoni numrin mbi simbolin e pjesëtimit me pjesëtuesin. Sillni rezultatin në fund të numrit të parë nën simbolin e ndarjes. Meqenëse 3 x 2 = 6, atëherë do ta ulni numrin 6 poshtë.
- Zbritni 2 numrat që keni shënuar. 6 - 6 = 0. Mund ta lini 0 bosh, sepse në përgjithësi nuk i filloni numrat me 0.
-
Sillni numrin e dytë që është nën simbolin e pjesëtimit.
- Pjestoni numrin që ulni me pjesëtuesin. Në këtë rast, 8/2 = 4. Shkruani numrin 4 mbi simbolin e pjesëtimit.
-
Shumëzoni numrin e sipërm të djathtë me pjesëtuesin dhe ulni numrin. 4 x 2 = 8.
-
Zbrit ato numra. Zbritja përfundimtare kthen zero, që do të thotë se e keni zgjidhur problemin. 68 x 2 = 34.

Hapi 3. Llogaritni edhe pjesën e mbetur
Disa nga pjesëtuesit nuk janë ndarë plotësisht në numra të tjerë. Nëse keni përfunduar zbritjen e fundit dhe nuk keni më numra për të nxjerrë, atëherë numri i fundit është pjesa e mbetur.






