Reciprok ose reciprok është shumë i dobishëm në të gjitha llojet e ekuacioneve algjebrike. Për shembull, kur ndani një thyesë me një tjetër, shumëzoni thyesën e parë me reciprokun e të dytit. Ju gjithashtu duhet të përdorni të kundërtën kur kërkoni ekuacionin e një linje.
Hapi
Metoda 1 nga 3: Gjetja e anasjellta e një thyese ose numër i plotë
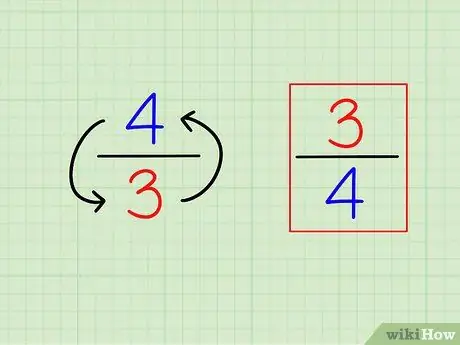
Hapi 1. Gjeni reciprokun e thyesës duke e përmbysur atë
Përkufizimi i "reciprok" ose i kundërt është shumë i lehtë. Për të gjetur reciprokun e çdo numri të plotë, thjesht llogaritni "1 (ai numër)". Për thyesat, reciprokja është një thyesë e ndryshme, domethënë, numrat janë "të përmbysur" (anasjelltas).
- Për shembull, e kundërta e 3/4 është 4/3.
- Çdo numër kur shumëzohet me kthimet e tij reciproke 1.
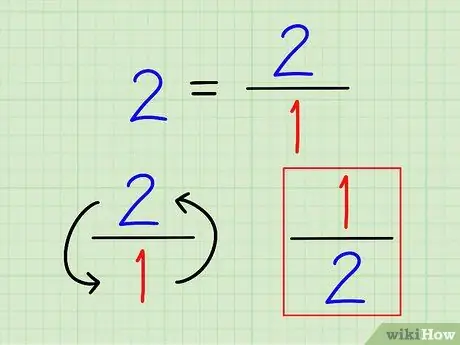
Hapi 2. Shkruani reciprokun e të gjithë numrit si thyesë
Përsëri, reciprokja e një numri është gjithmonë 1 (ai numër). Për numrat e plotë, shkruajini si thyesa. Nuk ka kuptim të llogarisim atë numër në një decimal.
Për shembull, reciprokja e 2 është 1 2 = 1/2.
Metoda 2 nga 3: Gjetja e anasjellta e një thyese të përzier
Hapi 1. Identifikoni numrat e përzier
Thyesat e përziera përbëhen nga numra të plotë dhe thyesa, të tilla si 24/5Me Ka dy hapa për të gjetur reciprokun e një numri të përzier siç përshkruhet më poshtë.
Hapi 2. Shndërroni numrat e përzier në thyesa të papërshtatshme
Mos harroni se 1 gjithmonë mund të shkruhet si (numër)/(i njëjti numër), dhe thyesat me të njëjtin emërues (numri i poshtëm) mund të shtohen së bashku. Këtu është një shembull duke përdorur 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
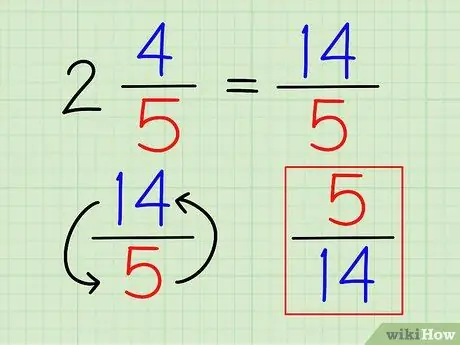
Hapi 3. Përmbysni thyesën
Pasi numri është shkruar plotësisht si një thyesë, ju mund ta gjeni reciprokun e tij ashtu si do të kishit çdo thyesë tjetër, duke e përmbysur thyesën.
Në shembullin e mësipërm, reciprok i 14/5 është 5/14.
Metoda 3 nga 3: Gjetja e së kundërtës së një dhjetore
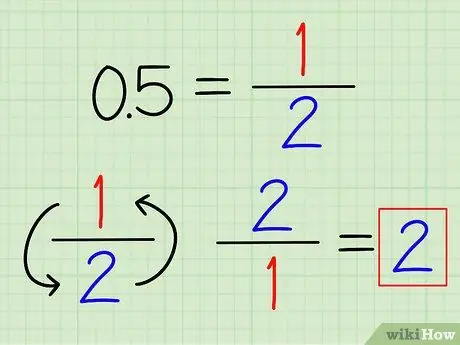
Hapi 1. Shndërroni numrat dhjetorë në thyesa nëse është e mundur
Ju mund të njihni disa numra dhjetorë të përdorur shpesh, të cilët mund të konvertohen lehtësisht në thyesa. Për shembull, 0.5 = 1/2 dhe 0.25 = 1/4Me Pasi dhjetorja është konvertuar në një thyesë, thjesht rrokullisni thyesën për të gjetur reciprokun e saj.
Për shembull, reciprokja e 0.5 është 2/1 = 2.
Hapi 2. Shkruani një problem të pjesëtimit
Nëse nuk mund ta konvertoni atë në një thyesë, llogaritni reciprokun e numrit në formën e një problemi të pjesëtimit: 1 (dhjetor). Ju mund të përdorni një kalkulator për ta zgjidhur atë ose të vazhdoni në hapin tjetër për ta zgjidhur atë me dorë.
Për shembull, mund të gjeni reciprokun e 0.4 duke llogaritur 1 0.4
Hapi 3. Ndryshoni problemin e pjesëtimit për të përdorur numra të plotë
Hapi i parë për ndarjen e numrave dhjetorë është lëvizja e pikës dhjetore derisa të gjithë numrat të jenë numra të plotë. Për sa kohë që lëvizni pikën dhjetore të të dy numrave me të njëjtin numër hapash, do të merrni përgjigjen e duhur.
Për shembull, mund të përdorni 1 0, 4 dhe ta rishkruani atë si 10 4. Në këtë rast, ju i zhvendosni të gjitha vendet dhjetore një hap në të djathtë, në të njëjtën mënyrë që shumëzoni secilin numër me dhjetë
Hapi 4. Zgjidh problemin duke përdorur ndarjen e gjatë
Përdorni metodën e ndarjes së gjatë për të llogaritur reciprokun. Nëse numëroni 10 4, do të merrni përgjigjen 2, 5 e cila është reciproke e 0, 4.
Këshilla
- Reciproca negative e një numri është e njëjtë me reciprokun e rregullt, në atë që shumëzohet me atë negativ. Për shembull, reciprokja negative e 3/4 eshte -4/3.
- Reciprok ose reciprok shpesh quhet "shumëzimi i anasjelltë".
- Numri 1 është e kundërta e vetvetes sepse 1 1 = 1.
- Numri 0 nuk ka reciprok sepse 0 është i papërcaktuar.
