Si të llogarisni shpejtësinë mesatare: 12 hapa (me fotografi)

2024 Autor: Jason Gerald | [email protected]. E modifikuara e fundit: 2024-02-01 14:15

E tëra çfarë ju nevojitet për të llogaritur shpejtësinë mesatare është zhvendosja totale. ose ndryshimi i pozicionit, dhe koha totale. Mos harroni se shpejtësia llogarit gjithashtu drejtimin dhe shpejtësinë e një objekti, kështu që përfshini një drejtim në përgjigjen tuaj, të tilla si "veri", "përpara" ose "majtas". Nëse problemi juaj i llogaritjes së shpejtësisë përfshin gjithashtu nxitim të vazhdueshëm, mund të mësoni një mënyrë të shpejtë për ta gjetur përgjigjen edhe më lehtë.

Hapi

Metoda 1 nga 2: Llogaritja e shpejtësisë mesatare të zhvendosjes dhe kohës

Hapi 1. Mos harroni se shpejtësia përfshin si shpejtësinë ashtu edhe drejtimin e një objekti

Shpejtësia përshkruan shkallën me të cilën ndryshon pozicioni i një objekti. Kjo ka të bëjë jo vetëm me shpejtësinë e lëvizjes së objektit, por edhe me drejtimin e tij. "100 metra për sekondë drejt jugut" është një vlerë e ndryshme e shpejtësisë sesa "100 metra për sekondë në lindje".

• Sasitë që kanë drejtim quhen madhësi vektoriale '. Kjo sasi mund të dallohet nga një sasi pa drejtim e quajtur sasi shkallore duke shkruar një shigjetë mbi ndryshoren. Për shembull, shënimi v përfaqëson normën, ndërsa shënimi v ^→ paraqet shpejtësinë ose shpejtësinë + drejtimin. Shënimi v i përdorur në këtë artikull përfaqëson shpejtësinë.
• Në problemet shkencore, duhet të përdorni njehsorë ose njësi të tjera metrike për të shprehur distancën, ndërsa për qëllime të përditshme mund të përdorni çdo njësi që ju pëlqen.

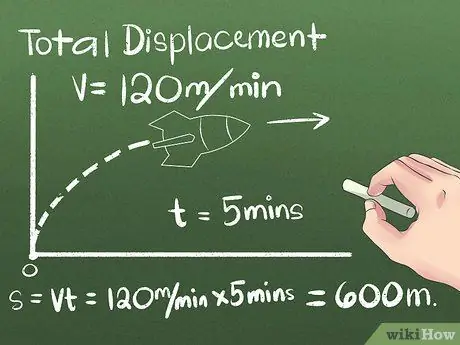
Hapi 2. Gjeni vlerën totale të zhvendosjes

Zhvendosja është ndryshimi në pozicionin e një objekti, ose distanca dhe drejtimi midis pikave të fillimit dhe mbarimit të tij. Drejtimi që objekti lëviz para se të arrijë pozicionin e tij përfundimtar mund të neglizhohet, sepse merret parasysh vetëm distanca midis pikave të fillimit dhe mbarimit. Për shembullin e parë, ne do të përdorim një objekt që lëviz me një shpejtësi konstante në një drejtim:

• Thuaj një raketë po lëviz në veri për 5 minuta me një shpejtësi konstante prej 120 metrash në minutë. Për të llogaritur pozicionin përfundimtar, përdorni formulën s = vt, ose përdorni mendimin praktik për të llogaritur distancën e përshkuar nga raketa pas kësaj (5 minuta) (120 metra/minutë) = 600 metra në veri nga pika e fillimit.
• Për problemet që përfshijnë nxitim të vazhdueshëm, mund t'i zgjidhni me s = vt + at², ose përdorni metodën e shkurtër të përshkruar në një seksion tjetër për të gjetur përgjigjen.

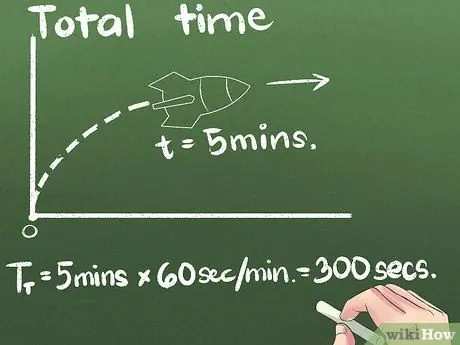
Hapi 3. Gjeni kohën totale të shpenzuar

Në shembullin tonë, raketa po ecën përpara për 5 minuta. Ju mund të shprehni shpejtësinë mesatare në çdo njësi të kohës, por e dyta është njësia standarde shkencore ndërkombëtare. Ne do të ndryshojmë njësitë e sekondave në këtë shembull: (5 minuta) x (60 sekonda/minutë) = 300 sekonda.

Edhe në problemet shkencore, nëse pyetja përdor orën ose një njësi më të madhe të kohës, do të jetë më e lehtë të llogarisni shpejtësinë së pari, pastaj të konvertoni përgjigjen përfundimtare në metra/sekondë

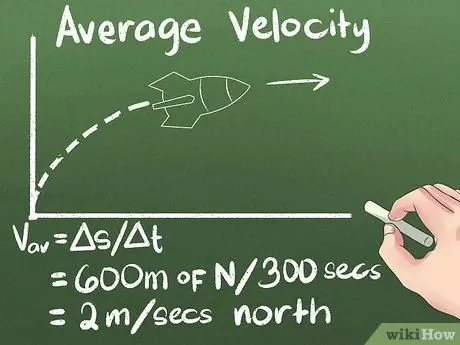
Hapi 4. Llogarit shpejtësinë mesatare si zhvendosje me kalimin e kohës

Nëse e dini se sa larg po lëviz një objekt dhe sa kohë do të marrë për të arritur atje, do ta dini se sa shpejt po lëviz. Pra, për shembullin që po përdorim, shpejtësia mesatare e raketës është (600 metra në veri) / (300 sekonda) = 2 metra/sekondë në veri.

• Mos harroni të përfshini një drejtim (të tillë si "para" ose "veri").
• Në formulën v_av = s/ΔtMe Simboli delta do të thotë "ndryshim", kështu që s/Δt do të thotë "ndryshim në pozicion gjatë një periudhe kohe".
• Shpejtësia mesatare mund të shkruhet si v_av, ose si v me një vijë horizontale mbi të.

Hapi 5. Zgjidhni probleme më të ndërlikuara

Nëse një objekt ndryshon drejtimin ose shpejtësinë e tij, mos u ngatërroni. Shpejtësia mesatare llogaritet "vetëm" nga zhvendosja totale dhe koha totale. Ajo që ndodh midis pikave të fillimit dhe mbarimit mund ta injoroni. Më poshtë janë disa shembuj të një objekti që udhëton me të njëjtën zhvendosje dhe kohë totale, dhe kështu, të njëjtën shpejtësi mesatare:

• Anna ecën në perëndim me 1 metër/s për 2 sekonda, pastaj papritmas përshpejtohet në 3 metra/sekondë dhe vazhdon ecjen në perëndim për 2 sekonda. Zhvendosja totale është (1 m/s në perëndim) (2 sek) + (3 m/s në perëndim) (2 sek) = 8 metra në perëndim. Koha totale është 2 sekonda + 2 sekonda = 4 sekonda. Pra, shpejtësia mesatare është 8 metra në perëndim/ 4 sekonda = 2 metra/sekondë në perëndim.

• Bart ecën në perëndim me 5 metra/sek për 3 sekonda, pastaj kthehet dhe ecën në lindje me 7 metra/sek për 1 sekondë. Ne mund të mendojmë për lëvizjen në lindje si "lëvizje negative drejt perëndimit" kështu që zhvendosja totale është = (5 metra/sek në perëndim) (3 sek) + (-7 m/s në perëndim) (1 sek) = 8 metra. Koha totale = 4 sekonda. Shpejtësia mesatare = 8 metra në perëndim / 4 sekonda = 2 metra/sekondë në perëndim.

• Charlotte eci në veri 1 metër dhe pastaj eci në perëndim 8 metra, pastaj në jug 1 metër. Koha që duhet për të përfunduar të gjithë udhëtimin është 4 sekonda. Vizatoni diagramin në një copë letër dhe do të shihni që pika përfundimtare është 8 metra në perëndim të pikës së fillimit, kështu që kjo vlerë është zhvendosja. Koha e përgjithshme që duhet është 4 sekonda, kështu që shpejtësia mesatare është 8 metra në perëndim / 4 sekonda = 2 metra/sekondë në perëndim.

  Metoda 2 nga 2: Llogaritja e Shpejtësisë Mesatare të Përshpejtimit Fiks

  

  Hapi 1. Merrni parasysh shpejtësinë fillestare dhe nxitimin konstant

  Le të themi se problemi ynë është "Një biçikletë po lëviz në të djathtë me një shpejtësi prej 5 m/s, me një nxitim konstant prej 2 m/s²Me Nëse kjo biçikletë lëviz për 5 sekonda, sa është shpejtësia mesatare e saj?"

  Nëse njësia "metër/sekondë²"për t'ju ngatërruar, shkruani atë si" metra/sekondë/sekondë "ose" metra për sekondë në sekondë. "Një nxitim prej 2 metrash/sekondë/sekondë do të thotë që shpejtësia po rritet me 2 metra në sekondë çdo sekondë.

  

  Hapi 2. Përdorni nxitimin për të gjetur shpejtësinë përfundimtare

  Përshpejtimi, i shënuar me shënimin a, është shkalla e ndryshimit të shpejtësisë (ose shkallës). Shpejtësia rritet me një rritje konstante. Ju mund të vizatoni një tabelë duke përdorur nxitimin për të gjetur shpejtësinë në kohë të ndryshme gjatë udhëtimit me biçikletë. Ne duhet të krijojmë këtë tabelë për të gjetur pikën përfundimtare të problemit (në t = 5 sekonda), por ne do të krijojmë një tabelë më të gjatë për ta bërë më të lehtë për ju që të kuptoni këtë koncept:

  • Në pikën e fillimit (koha t = 0 sekonda), biçikleta po lëviz me një shpejtësi prej 5 metrash/s.
  • Pas 1 sekonde (t = 1), biçikleta po lëviz me një shpejtësi prej 5 metrash/sekondë + me = 5 metra/sekondë + (2 metra/sekondë²) (1 sekondë) = 7 metra/sekondë.
  • Në t = 2, biçikleta po lëviz në të djathtë me një shpejtësi prej 5+ (2) (2) = 9 metra/sek.
  • Në t = 3, biçikleta po lëviz në të djathtë me një shpejtësi prej 5+ (2) (3) = 11 metra/sek.
  • Në t = 4, biçikleta po lëviz në të djathtë me një shpejtësi prej 5+ (2) (4) = 13 metra/sek.
  • Në t = 5, biçikleta po lëviz në të djathtë me një shpejtësi 5+ (2) (5) = 15 metra/sekondë.

  

  Hapi 3. Përdorni këtë formulë për të gjetur shpejtësinë mesatare

  Nëse dhe "vetëm" nëse nxitimi është konstant, shpejtësia mesatare do të jetë e barabartë me vlerën mesatare të shumës së shpejtësive përfundimtare dhe fillestare. (v_f +v_une)/2Me Për shembullin tonë të problemit më lart, shpejtësia fillestare e biçikletës është v_une 5 metra/sekondë. Pasi të llogarisim, shpejtësia përfundimtare është v_f 15 metra/sekondë. Duke i shtuar këto dy vlera së bashku, marrim (15 metra/sekondë + 5 metra/sekondë)/2 = (20 metra/sekondë)/2 = 10 metra/drejtimi i dytë i djathtë.

  • Mos harroni të përfshini drejtimin, në këtë rast "të drejtë".
  • Ky term mund të shkruhet si v₀ (shpejtësia në kohën 0, ose shpejtësia fillestare) dhe v (shpejtësia përfundimtare).

  

  Hapi 4. Kuptoni formulën e shpejtësisë mesatare në mënyrë intuitive

  Për të gjetur shpejtësinë mesatare, ne mund ta përdorim shpejtësinë në çdo pikë dhe të gjejmë mesataren për të gjitha. (Ky është përkufizimi i mesatares.) Meqenëse kjo kërkon llogaritje ose kohë të pafundme, kuptojeni këtë formulë në mënyrë më intuitive. Në vend që të merrni çdo herë, llogaritni shpejtësinë mesatare të dy pikave kohore dhe shihni rezultatet. Një pikë në kohë është afër fillimit të udhëtimit, ku biçikleta po ecën ngadalë, dhe një pikë tjetër është pranë pikës përfundimtare ku biçikleta po ecën me shpejtësi.

  

  Hapi 5. Provoni teorinë intuitive

  Përdorni tabelën e mësipërme për të përcaktuar shpejtësinë në pika të ndryshme kohore. Disa çifte që plotësojnë kriteret tona janë (t = 0, t = 5), (t = 1, t = 4), ose (t = 2, t = 3). Ju mund ta provoni këtë formulë me vlera t të tjera përveç numrave të plotë, nëse dëshironi.

  Cilado palë pikash që zgjidhni, shpejtësia mesatare në atë kohë do të jetë gjithmonë e njëjtë. Për shembull, ((5+15)/2), ((7+13)/2), ose ((9+11)/2) të gjitha të barabarta 10 metra/sek në të djathtë

  

  Hapi 6. Plotësoni shpjegimin intuitiv

  Nëse e përdorim këtë metodë me një listë të çdo kohe të marrë, ne do të vazhdojmë të llogarisim mesataren e gjysmës së parë të udhëtimit dhe gjysmës së dytë të udhëtimit. Koha që duhet për të mbuluar secilën gjysmë është e njëjtë, kështu që asnjë shpejtësi nuk humbet kur të përfundojmë numërimin.

  • Meqenëse secila çift do të japë të njëjtin rezultat, mesatarja e këtyre shpejtësive do të jetë gjithashtu e njëjtë në vlerë. Në shembullin tonë, shpejtësia e tërësisë është "10 metra/sek djathtas" do të jetë akoma 10 metra/sek djathtas.
  • Ne mund ta gjejmë këtë vlerë duke llogaritur mesataren e çdo çifti, për shembull shpejtësitë fillestare dhe përfundimtare. Në shembullin tonë, këto shpejtësi arrihen në t = 0 dhe t = 5, dhe mund të llogariten duke përdorur formulën e mësipërme: (5+15)/2 = 10 metra/sek në të djathtë.

  

  Hapi 7. Kuptoni këtë formulë matematikisht

  Nëse jeni më të kënaqur me provat e shkruara si formula, mund të filloni me një formulë për të llogaritur distancën e përshkuar duke supozuar nxitim konstant, dhe nxirrni formulën prej andej:

  • s = v_unet + në²Me (Teknikisht s dhe t, ose ndryshoni pozicionin dhe ndryshoni në kohë, por do të kuptoheshit po të kishit shkruar s dhe t.)
  • Shpejtësia mesatare v_av përcaktohet si s/t, kështu që futni formulën në formën s/t.
  • v_av = s/t = v_une + në
  • Koha e përshpejtimit x është e barabartë me ndryshimin e shpejtësisë totale, ose v_f - v_uneMe Pra, ne mund të zëvendësojmë "at" në formulë, dhe të marrim:
  • v_av = v_une + (v_f - v_une).
  • Thjeshtoni: v_av = v_une + v_f - v_une = v_une + v_f = (v_f +v_une)/2.

  Këshilla

  • Shpejtësia është e ndryshme nga shpejtësia sepse shpejtësia është një madhësi vektoriale ndërsa shpejtësia është një madhësi shkallore. Madhësitë vektoriale përfshijnë drejtimin dhe madhësinë, ndërsa madhësitë shkallore përfshijnë vetëm madhësinë.
  • Nëse objekti lëviz në një dimension, siç është majtas-djathtas, mund të përdorni një numër pozitiv për të përfaqësuar një drejtim (siç është e djathta) dhe një numër negativ për të përfaqësuar një drejtim tjetër (majtas). Shkruani këtë shënim në krye të faqes tuaj në mënyrë që të jetë e qartë për njerëzit që lexojnë punën tuaj.