- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- E modifikuara e fundit 2025-01-23 12:47.
Shtimi dhe zbritja e thyesave është një aftësi e rëndësishme që keni. Thyesat shfaqen në jetën e përditshme gjatë gjithë kohës, veçanërisht në klasat e matematikës, nga fillorja në kolegj. Ndiqni këto hapa për të mësuar se si të shtoni dhe zbritni thyesa, nga thyesa ekuivalente, thyesa të pabarabarta, numra të përzier ose thyesa të zakonshme. Nëse e dini tashmë një mënyrë, është vërtet e lehtë të zgjidhni fraksionet e tjera!
Hapi
Metoda 1 nga 4: Shtimi dhe zbritja e thyesave me emëruesin e njëjtë
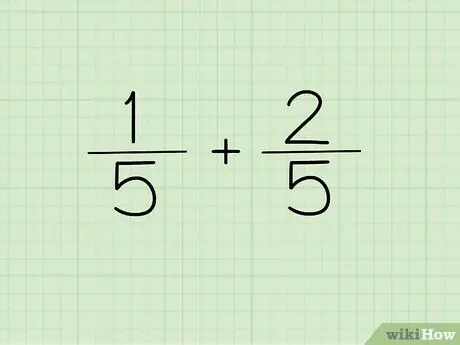
Hapi 1. Shkruani pyetjen tuaj
Nëse emëruesi i dy thyesave që dëshironi të shtoni ose zbritni është i njëjtë, shkruani emëruesin një herë si emërues të përgjigjes suaj.
Me fjalë të tjera, 1/5 dhe 2/5 nuk duhet të shkruhen si 1/5 + 2/5 =?, por mund të shkruhet si (1+2)/5 =? Me Emëruesit janë të njëjtë, kështu që ato mund të shkruhen vetëm një herë. Dy numruesit janë të kombinuar
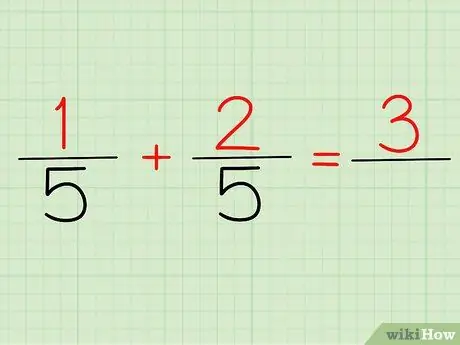
Hapi 2. Shtoni numëruesit
Numëruesi është numri që është mbi çdo thyesë. Nëse shikojmë problemin e mësipërm, 1/5 dhe 2/5, 1 dhe 2 janë numëruesit tanë.
Pavarësisht nëse e shkruani 1/5 + 2/5 ose (1 + 2)/5, përgjigjja juaj do të jetë e njëjtë: 3! Sepse, 1 + 2 = 3

Hapi 3. Lëreni emëruesin
Meqenëse emëruesit janë të njëjtë, mos bëni asgjë me emëruesit! Mos shtoni, zbritni, shumëzoni ose ndani. Lëre të jetë.
Pra, nga i njëjti shembull, emëruesi ynë është 5. E drejtë! 5 është numri i fundit i thyesës sonë. Ne kemi gjysmën e përgjigjes

Hapi 4. Shkruani përgjigjen tuaj
Tani, gjithçka që duhet të bëni është të shkruani numëruesin dhe emëruesin tuaj! Nëse përdorni shembullin e mësipërm, përgjigjja juaj do të jetë 3/5.
Cili është numëruesi juaj? 3. Emëruesi juaj? 5. Prandaj, 1/5 + 2/5 ose (1 + 2)/5 është e barabartë me 3/5.
Metoda 2 nga 4: Shtimi dhe zbritja e thyesave me emërues të ndryshëm

Hapi 1. Gjeni emëruesin më të vogël të përbashkët
Kjo do të thotë, emëruesi më i vogël është i njëjtë për të dy thyesat. Supozoni se kemi thyesat 2/3 dhe 3/4. Cili është emëruesi? 3 dhe 4. Për të gjetur emëruesin më të vogël të përbashkët të të dy thyesave, mund ta bëni këtë në tre mënyra:
- Shkruani shumëfishat e. Shumëfishat e 3 janë 3, 6, 9, 12, 15, 18… dhe kështu me radhë. Shumëfishi i 4? 4, 8, 12, 16, 20, dhe kështu me radhë. Cili është numri më i vogël që është shumëfish i të dyve? 12! Ky është emëruesi më pak i zakonshëm.
-
Faktorizimi kryesor. Nëse dini për faktorët, mund të bëni faktorizimin kryesor. Kjo do të thotë, ju po kërkoni numrat që përbëjnë emëruesin tuaj. Për numrin 3, faktorët janë 3 dhe 1. Për numrin 4, faktorët janë 2 dhe 2. Pastaj, të gjithë ju. 3 x 2 x 2 = 12. Emëruesi juaj më i vogël i përbashkët!
Shumëzoni të gjithë numrat për numrin më të vogël. Në disa probleme, si ky, ju mund të shumëzoni të dy numrat - 3 x 4 = 12. Megjithatë, nëse keni një emërues të madh, mos e bëni këtë! Ju nuk doni të shumëzoni 56 x 44 dhe të dilni për të marrë 2,464

Hapi 2. Shumëzoni emëruesin me numrin e nevojshëm për të marrë emëruesin më të vogël të përbashkët
Me fjalë të tjera, ju dëshironi që të gjithë emëruesit tuaj të jenë të barabartë. Në shembullin tonë, ne duam që emëruesi të jetë 12. Për të ndryshuar 3 në 12, ju shumëzoni 3 me 4. Për të ndryshuar 4 në 12, ju shumëzoni 4 me 3. I njëjti emërues do të jetë emëruesi i përgjigjes suaj përfundimtare.
-
Pra 2/3 bëhet 2/3 x 4 dhe 3/4 bëhet 3/4 x 3. Domethënë, tani kemi 2/12 dhe 3/12. Por, ne nuk kemi mbaruar akoma!
- Do të vini re se emëruesit shumëzohen me njëri -tjetrin. Kjo mund të bëhet në këtë situatë, por jo në të gjitha situatat. Ndonjëherë, në vend që të shumëzoni të dy emëruesit, mund t'i shumëzoni të dy emëruesit me një numër tjetër për të marrë numrin më të vogël.
- Pastaj në probleme të tjera, ndonjëherë ju vetëm duhet të shumëzoni një emërues për ta bërë atë të barabartë me emëruesin e thyesës tjetër në problem.

Hapi 3. Shumëzoni numëruesin me të njëjtin numër
Kur shumëzoni emëruesin me një numër, duhet gjithashtu të shumëzoni numëruesin me të njëjtin numër. Ajo që bëmë në hapin e fundit është vetëm një pjesë e shumëzimit që duhet bërë.
Ne kemi 2/3x4 dhe 2/4x3 si hapin e parë - pastaj, në hapin e dytë, 2 x 4/3 x 4 dhe 3 x 3/4 x 3. Domethënë, numrat tanë të rinj janë 8/12 dhe 9/ 12 Perfekte
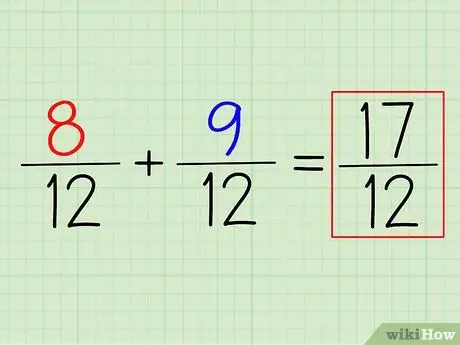
Hapi 4. Shtoni (ose zbritni) numëruesit për të marrë përgjigjen
Për të shtuar 8/12 + 9/12, gjithçka që duhet të bëni është të shtoni numëruesit. Mos harroni: thjesht lini emëruesin. Emëruesi më i vogël i përbashkët që gjeni është emëruesi juaj përfundimtar.
Në këtë shembull, (8+9)/12 = 17/12. Për ta kthyer atë në një numër të përzier, thjesht zbritni emëruesin nga numëruesi dhe shkruani pjesën e mbetur. Në këtë rast, 17/12 = 1 5/12
Metoda 3 nga 4: Shtimi dhe zbritja e thyesave të përziera dhe të zakonshme
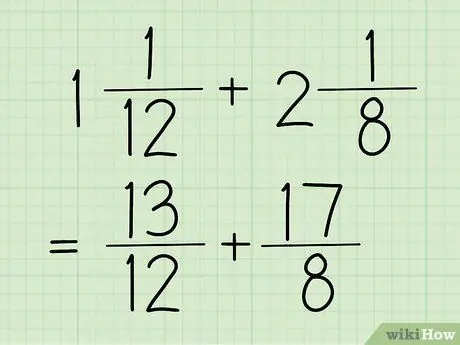
Hapi 1. Shndërroni thyesat tuaja të përziera në thyesa të zakonshme
Një numër i përzier është një thyesë që ka një numër të plotë dhe një thyesë, si në shembullin e mësipërm (1 5/12). Ndërkohë, një thyesë e zakonshme është një thyesë, numëruesi i të cilit (numri i lartë) është më i madh se emëruesi (numri i poshtëm). Ky fraksion shihet gjithashtu në hapin e mëparshëm, i cili është 17/12.
Për shembujt në këtë pjesë, ne do të përdorim 13/12 dhe 17/8

Hapi 2. Gjeni një emërues të përbashkët
A i mbani mend tre mënyrat për të gjetur emëruesin më të vogël të përbashkët? Duke shkruar shumëfish, duke përdorur faktorizimin kryesor ose duke shumëzuar emëruesit.
Le të gjejmë shumëfishin e shembullit tonë, 12 dhe 8. Cili është numri më i vogël që të dy kanë të përbashkët? 24 8, 16, 24 dhe 12, 24 - bingo

Hapi 3. Shumëzoni numëruesin dhe emëruesin tuaj për të gjetur thyesën ekuivalente
Të dy emëruesit duhet të ndryshohen në 24. Si i konvertoni 12 në 24? Shumëzoni me 2. 8 në 24? Shumëzoni me tre. Por mos harroni - duhet të shumëzoni edhe numëruesit!
Pra (13 x 2)/(12 x 2) = 26/24. Dhe (17 x 3)/(8 x 3) = 51/24. Kemi mbaruar me këtë

Hapi 4. Shtoni ose zbritni thyesat tuaja
Tani që keni të njëjtin emërues, mund t'i shtoni me lehtësi dy numëruesit së bashku. Mos harroni, thjesht lini emëruesin!
26/24 + 51/24 = 77/24. Kjo është shuma juaj! Sidoqoftë, numrat në krye ishin shumë të mëdhenj…

Hapi 5. Ktheni përgjigjen tuaj në numra të përzier
Numri shumë i madh në krye të thyesës ndihet pak i çuditshëm - ju nuk mund të tregoni madhësinë e fraksionit tuaj. E tëra çfarë ju duhet të bëni është të zbritni emëruesin tuaj nga numëruesi në mënyrë të përsëritur derisa të mos zbritet më tej dhe të shkruani pjesën e mbetur.
-
Në këtë shembull, 77 minus 24 me 3 herë. Kjo do të thotë, 24 x 3 = 72. Pjesa e mbetur është 5! Pra cili është rezultati juaj përfundimtar? 3 5/24.
Shumë e vërtetë!
Metoda 4 nga 4: Shtoni dhe Zbritni thyesat pa gjetur LCM
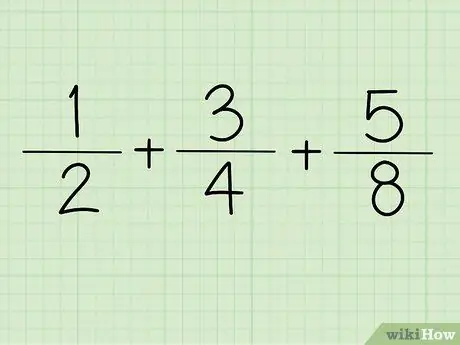
Hapi 1. Shkruani thyesën
Për shembull + +

Hapi 2. Zgjidhni së pari numëruesin
- Shumëzojeni me numëruesin e thyesës tjetër.
- Shumëzoni 1 me 4 dhe 8. [32]
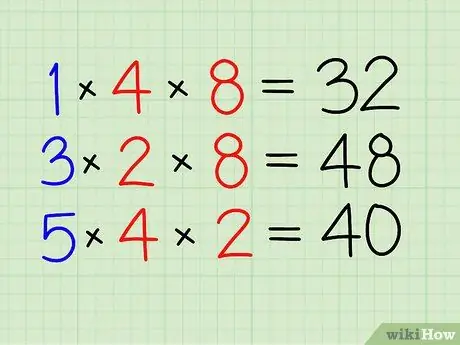
Hapi 3. Bëni të njëjtën gjë për thyesat e tjera
- Shumëzoni 3 me 2 dhe 8. [48]
- Së fundi, shumëzoni 5 me 4 dhe 2. [40]
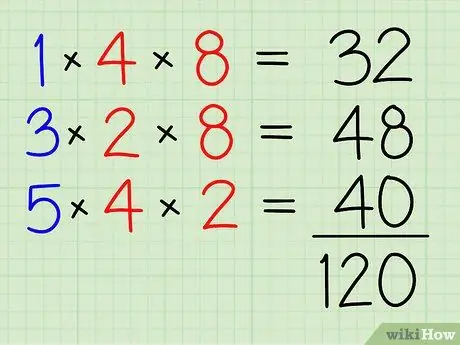
Hapi 4. Shtojini të gjitha së bashku
32+48+40=120
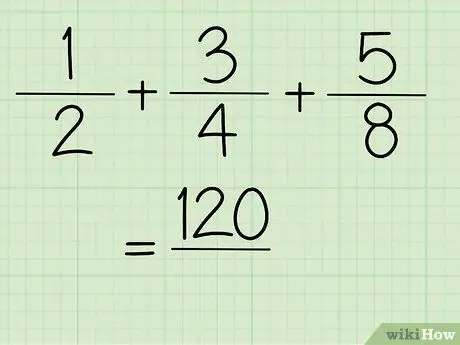
Hapi 5. Tani, ju merrni vlerën e numëruesit

Hapi 6. Zgjidhni emëruesin e thyesës

Hapi 7. Shumëzoni të gjithë emëruesit e thyesave
2×4×8=64

Hapi 8. Tani, ju merrni rezultatin
120/64 = 1 56/64 = 1 ⅞
Paralajmërim
- Kjo metodë ju lejon të shumëzoni numra të mëdhenj.
- Ju mund të keni nevojë për një kalkulator për të llogaritur në këtë mënyrë.






