- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- E modifikuara e fundit 2025-01-23 12:47.
Studentët që janë ende shumë të rinj shpesh kanë vështirësi të kuptojnë konceptin e zbritjes. Nëse jeni mësues dhe doni t'u mësoni nxënësve konceptin e zbritjes, përpiquni të përfaqësoni konceptin në një mënyrë interesante dhe më të kuptueshme për studentët. Pasi të keni shpjeguar konceptet themelore të zbritjes, provoni të kaloni në konceptin e zbritjes dyshifrore. Pasi studentët ta kenë përvetësuar mirë, provoni të shpjegoni koncepte të ndryshme që mund të përdorin për të zgjidhur problemet e zbritjes, siç është Bërthama e Përbashkët.
Hapi
Metoda 1 nga 4: Mësimi i zbritjes përmes objekteve ose imazheve

Hapi 1. Shkruani ose paraqitni me gojë një problem të historisë që përmban një problem të zbritjes për studentët:
Ka 8 portokall në tryezë, 3 portokall i ha Jordania. Sa portokall kanë mbetur?
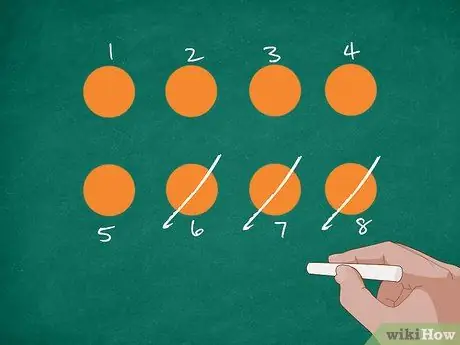
Hapi 2. Paraqitni problemin me figura
Së pari, vizatoni 8 rrathë portokalli në tabelë ose një copë letër. Pas kësaj, lërini studentët të numërojnë numrin dhe të etiketojnë secilin rreth me një numër. Kryqëzoni 3 qarqe ndërsa shpjegoni se Jordan hëngri 3 portokall. Pyetini studentët sa portokall kanë mbetur tani.
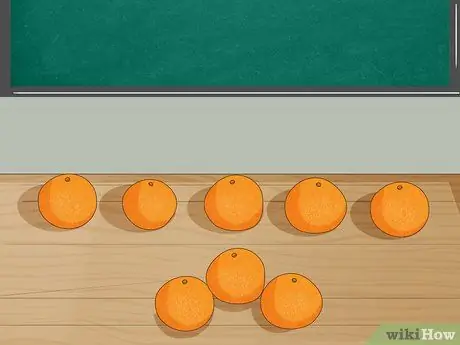
Hapi 3. Paraqitni problemin me objekte
Vendosni 8 portokalle në tryezë dhe kërkoni nga studentët të numërojnë numrin. Pas kësaj, merrni 3 portokalle nga tryeza ndërsa shpjegoni se Jordan hëngri 3 portokall. I bëni studentët të numërojnë numrin e portokalleve të mbetur.

Hapi 4. Shkruani ekuacionin
Shpjegoni se problemet e historisë gjithashtu mund të përfaqësohen përmes një ekuacioni. Sigurohuni që t'i udhëzoni gjithmonë në procesin e shndërrimit të problemeve të tregimit në ekuacione matematikore.
- Pyesni sa portokall janë në tryezë. Shkruani numrin "8" në tabelë.
- Pyesni sa portokalle hëngri Jordania. Shkruani numrin "3" në tabelë.
- Pyetini studentët nëse ky është një problem me mbledhjen ose zbritjen. Shkruani një shenjë "-" midis numrave "8" dhe "3".
- I bëni studentët të kërkojnë përgjigje për ekuacionin “8-3”. Shkruani një shenjë "=" të ndjekur nga numri "5".
Metoda 2 nga 4: Mësimi i Zbritjes me Metodën e Numërimit në Linjën Numrore

Hapi 1. Shkruani ose paraqitni me gojë një problem të historisë që përmban një problem të zbritjes për studentët:
Ka 10 qen në dyqanin e kafshëve shtëpiake, 6 prej të cilëve janë birësuar nga pronarët e tyre të rinj. Sa qen kanë mbetur në dyqanin e kafshëve shtëpiake?
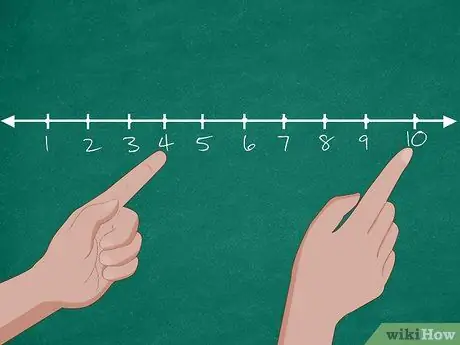
Hapi 2. Përdorni ndihmën e një linje numerike për të zgjidhur problemin
Së pari, vizatoni një vijë numerike që përmban numrat 0-10 në tabelë. Pas kësaj, kërkojuni studentëve të përmendin numrin e qenve në dyqanin e kafshëve shtëpiake. Pasi studentët të përgjigjen, rrethoni numrin "10" në tabelë. Pastaj, pyetni përsëri sa qen janë birësuar. Nëse studentët përgjigjen "6", kërkojuni atyre të numërojnë 6 numra nga 10 (9, 8, 7, 6, 5, 4) derisa të arrijnë numrin "4". Pas kësaj, pyesni përsëri sa qen kanë mbetur në dyqanin e kafshëve shtëpiake.

Hapi 3. Shkruani ekuacionin
Shpjegoni se problemet e historisë gjithashtu mund të përfaqësohen përmes një ekuacioni. Sigurohuni që t'i udhëzoni gjithmonë në procesin e shndërrimit të problemeve të historisë në ekuacione matematikore.
- Pyesni sa qen ka në dyqanin e kafshëve shtëpiake. Shkruani numrin "10" në tabelë.
- Pyesni sa qen janë birësuar. Shkruani numrin "6" në tabelë.
- Pyetini studentët nëse ky është një problem me mbledhjen ose zbritjen. Shkruani një shenjë "-" midis numrave "10" dhe "6".
- I bëni studentët të kërkojnë përgjigje për ekuacionin “10-6”. Shkruani një shenjë "=" të ndjekur nga numri "4."
Metoda 3 nga 4: Mësimi i Zbritjes përmes Koncepteve të Faktit të Familjes

Hapi 1. Prezantoni nxënësit konceptin e familjes së fakteve
Në fakt, një familje faktesh është një grup problemesh matematikore që përbëhen nga numra të njëjtë. Për shembull, numrat 10, 3 dhe 7 formojnë një familje faktesh. Tre numrat mund të shtohen ose zbriten në mënyra të ndryshme; Ju mund të gjeneroni dy ekuacione duke përdorur vetëm këta 3 numra:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Hapi 2. Shkruani ose paraqitni me gojë një problem të historisë që përmban një problem të zbritjes për studentët:
Kam 7 karamele. Nëse ha 3 karamele, sa karamele kanë mbetur?

Hapi 3. Përdorni konceptin e familjes fakt për të zgjidhur problemin
Drejtojini studentët hap pas hapi përmes procesit:
- Pyetini studentët se çfarë problemi do të donin të zgjidhnin. Shkruani "7-3 =?" në dërrasën e zezë.
- Kërkojuni atyre të identifikojnë anëtarin e tretë të grupit të faktit të familjes. Shkruani ekuacionet e mëposhtme në tabelë: “3+_ = 7”; "_+3 = 7"; "; "7 -_ = 3"; dhe 7-3 = _”Pas kësaj, kërkojuni studentëve të lexojnë rezultatet dhe të plotësojnë problemin me përgjigjet që ata dhanë.
Metoda 4 nga 4: Prezantimi i koncepteve të përbashkëta bazë
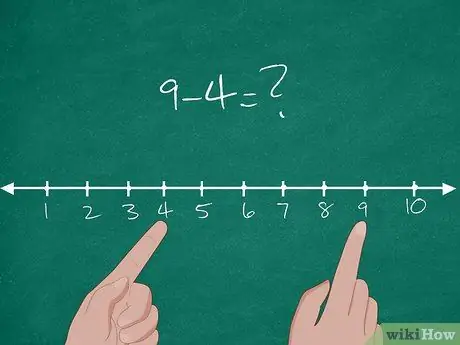
Hapi 1. Mësoni konceptin e zbritjes në Common Core
Në fakt, Common Core është një standard i ri mësimi që zbatohet nga shumica e shteteve në Amerikë. Në Common Core, koncepti bazë i zbritjes shpjegohet me distancën midis dy numrave. Për t’i shpjeguar konceptin nxënësve, provoni të vizatoni një tabelë numrash që përmban numrat 1-10 në tabelë.
- Pas kësaj, jepni një problem bazë zbritjeje studentëve: 9-4 = ?.
- Gjeni vendndodhjen e numrit 4 në rreshtin e numrave. Shpjegojuni studentëve se ky vend është pikënisja e tyre.
- Gjeni vendndodhjen e numrit 9 në rreshtin numerik. Shpjegojuni studentëve se vendi është destinacioni përfundimtar.
- Pas kësaj, kërkoni nga studentët të matin ose llogaritin distancën midis dy numrave: "5, 6, 7, 8, 9".
- Distanca midis dy numrave është 5. Kështu, 9-4 = 5.
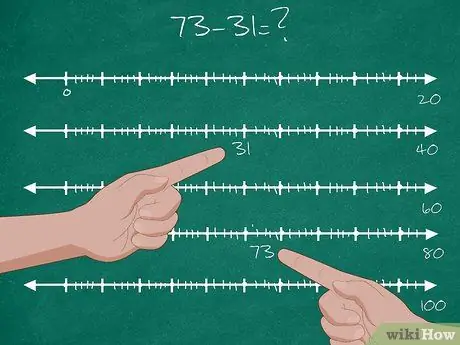
Hapi 2. I bëni nxënësit të zgjidhin problemin e zbritjes dyshifrore
Shpjegojuni studentëve se do të ketë dy pika që ata duhet të ndalojnë para se të mbërrijnë në destinacionin e tyre.
- Jepuni nxënësve një problem me zbritje dyshifrore: 73-31 = ?.
- Gjeni vendndodhjen e numrit 31 në rreshtin numerik. Kjo është pika e fillimit.
- Gjeni vendndodhjen e numrit 73 në rreshtin numerik. Ky është qëllimi përfundimtar.
- "Ndal" në të dhjetën e parë pas 31. Kështu, ndalesa juaj e parë është 40. Pas kësaj, matni distancën midis 31 dhe 40 dhe shkruani përgjigjen: 9.
- "Ndal" në të dhjetat që janë më afër 73. Kështu, ndalesa juaj e dytë është 70. Pastaj, matni distancën midis 40 (ndalesa e parë) dhe 70 (ndalesa e dytë) dhe shkruani përgjigjen: 30.
- "Lëviz" nga 70 (ndalesa e dytë) në destinacionin tuaj përfundimtar (73). Matni distancën mes tyre dhe shkruani përgjigjen: 3.
- Shtoni këto tre rezultate së bashku: 9+30+3 = 42. Kështu, 73-31 = 42.

Hapi 3. Kërkojuni nxënësve të zgjidhin problemin e zbritjes me tre shifra
Kur zgjidhni problemet e zbritjes dyshifrore, shpjegojini studentëve se ajo që do të rritet nuk janë vetëm ndalesat, por edhe distanca midis secilës ndalesë.
- Jepuni nxënësve një problem me zbritje tre shifrore: 815-398 = ?.
- Gjeni vendndodhjen e numrit 398 në rreshtin e numrave. Kjo është pika e fillimit.
- Gjeni vendndodhjen e numrit 815 në rreshtin numerik. Ky është qëllimi përfundimtar.
- "Ndal" në të dhjetën e parë pas 398. Kështu, ndalesa juaj e parë është 400. Matni distancën midis 398 dhe 400 dhe shkruani përgjigjen: 2.
- "Ndal" në të dhjetat që janë më afër 815. Pra ndalesa juaj e dytë është 800. Matni distancën midis 400 dhe 800 dhe shkruani përgjigjen: 400.
- "Ndal" në të dhjetat që janë më afër 815. Kështu, ndalesa juaj e tretë është 810. Matni distancën midis 800 dhe 810 dhe shkruani përgjigjen: 10.
- "Lëvizni" nga ndalesa e tretë në destinacionin tuaj përfundimtar, që është numri 815. Matni distancën dhe shkruani përgjigjen: 5.
- Shtoni të gjithë numrat që merrni: 2+400+10+5 = 417. Kështu, 815-398-417.






