- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- E modifikuara e fundit 2025-01-23 12:47.
Vlera P është një matje statistikore që ndihmon shkencëtarët të përcaktojnë nëse hipoteza e tyre është e saktë. Vlera P përdoret për të përcaktuar nëse rezultatet e eksperimentit të tyre janë brenda kufirit të vlerave që janë normale për gjërat e studiuara. Zakonisht, nëse vlera P e një grupi të dhënash bie nën një vlerë të caktuar të paracaktuar (për shembull, 0.05), shkencëtarët do të hedhin poshtë hipotezën zero të eksperimentit të tyre - me fjalë të tjera, ata do të përjashtojnë një hipotezë ku variabla eksperimentale ka asnjë efekt domethënës. në rezultat. Sot, vlerat p zakonisht gjenden në tabelat e referencës duke llogaritur vlerën e katrorit chi.
Hapi

Hapi 1. Përcaktoni rezultatet e pritshme të eksperimentit tuaj
Zakonisht, kur shkencëtarët kryejnë një eksperiment dhe shqyrtojnë rezultatet, ata tashmë kanë një ide për rezultatet normale ose të zakonshme paraprakisht. Kjo mund të bazohet në rezultatet e eksperimenteve të mëparshme, grupe të besueshme vëzhgimi, literaturë shkencore dhe/ose burime të tjera. Për eksperimentin tuaj, përcaktoni rezultatin tuaj të pritshëm dhe shkruani atë si një numër.
Shembull: Supozoni se një studim i mëparshëm tregoi se, në nivel kombëtar, biletat e shpejtësisë u lëshoheshin më shpesh makinave të kuqe sesa makinave blu. Supozoni se rezultati mesatar në nivel kombëtar tregon një raport 2: 1 me raportin e makinave të kuqe që është më shumë. Ne duam të zbulojmë nëse policia në qytetin tonë ka të njëjtën tendencë duke analizuar biletën e shpejtësisë të lëshuar nga policia në qytetin tonë. Nëse do të merrnim një mostër të rastësishme prej 150 biletash me shpejtësi të madhe të dhëna për makinat e kuqe dhe blu në qytetin tonë, do të prisnim 100 për makinë të kuqe dhe 50 për makinat blu nëse njësia e policisë në qytetin tonë jep një biletë sipas krahasimit në nivel kombëtar.

Hapi 2. Përcaktoni vëzhgimet tuaja eksperimentale
Tani që keni përcaktuar vlerën tuaj të pritshme, mund të drejtoni eksperimentin tuaj dhe të gjeni vlerën (ose vëzhgimin) e vërtetë. Përsëri, shënoni rezultatin si një numër. Nëse manipulojmë disa kushte eksperimentale dhe rezultatet e vëzhguara ndryshojnë nga rezultatet e pritura, ekzistojnë dy mundësi: ose kjo ka ndodhur rastësisht, ose ishte manipulimi ynë i variablave eksperimentalë që shkaktuan këtë ndryshim. Qëllimi i gjetjes së vlerës p është në thelb të përcaktojë nëse rezultatet e vëzhguara ndryshojnë nga rezultatet e pritura në një pikë ku hipoteza zero-hipoteza se nuk ka lidhje midis ndryshores eksperimentale dhe rezultateve të vëzhguara-nuk mund të hidhet poshtë.
Shembull: Supozoni, në qytetin tonë, ne zgjedhim rastësisht 150 bileta me shpejtësi që u jepen makinave të kuqe dhe blu. Ne marrim 90 një biletë për një makinë të kuqe dhe 60 për makinën blu. Kjo është e ndryshme nga rezultati që prisnim dmth 100 dhe 50Me A ka shkaktuar ndonjë ndryshim në rezultatet tona manipulimi ynë eksperimental (në këtë rast, ndryshimi i burimit të të dhënave nga kombëtar në lokal), apo policia jonë e qytetit kishte të njëjtat tendenca si niveli kombëtar, dhe ne vetëm vumë re rastësi? Vlera p do të na ndihmojë ta përcaktojmë atë.

Hapi 3. Përcaktoni shkallët e lirisë për eksperimentin tuaj
Shkallët e lirisë janë një masë e sasisë së ndryshueshmërisë në studim, e cila përcaktohet nga numri i kategorive që shqyrtoni. Ekuacioni për shkallët e lirisë është Shkallët e lirisë = n-1, ku n është numri i kategorive ose variablave të analizuar në eksperimentin tuaj.
-
Shembull: Eksperimenti ynë ka dy kategori rezultatesh: një për makinën e kuqe dhe një për makinën blu. Kështu, në eksperimentin tonë, kemi 2-1 = 1 shkallë lirie.
Nëse krahasojmë makina të kuqe, blu dhe jeshile, do të kemi
Hapi 2. shkallët e lirisë dhe kështu me radhë.

Hapi 4. Krahasoni rezultatet e pritura me rezultatet e vëzhguara duke përdorur katrorin chi
Katrori Chi (shkruar x2) është një vlerë numerike që mat ndryshimin midis vlerave të pritshme dhe të vëzhguara nga eksperimenti. Ekuacioni për katrorin chi është: x2 = ((o-e)2/e), ku o është vlera e vëzhguar dhe e është vlera e pritur. Shtoni rezultatet e këtij ekuacioni për të gjitha rezultatet e mundshme (shih më poshtë).
- Vini re se ky ekuacion përdor operatorin (sigma). Me fjalë të tjera, ju duhet të llogaritni ((| o-e | -.05)2/e) për secilin rezultat të mundshëm, pastaj shtoni rezultatet për të marrë vlerën e katrorit chi. Në shembullin tonë, ne kemi dy rezultate - një makinë që merr një biletë të kuqe ose një blu. Kështu, ne mund të llogarisim ((o-e)2/e) dy herë - një herë për makinën e kuqe dhe një herë për makinën blu.
-
Shembull: Le t'i lidhim vlerat dhe vëzhgimet tona të pritshme në ekuacionin x2 = ((o-e)2/e) Mos harroni se, për shkak të operatorit sigma, ne duhet të llogarisim ((o-e)2/e) dy herë - një herë për makinën e kuqe dhe një herë për makinën blu. Hapat e përpunimit janë si më poshtë:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Hapi 5. Zgjidhni një nivel rëndësie
Tani që ne e dimë shkallën e lirisë së pajisjes sonë eksperimentale dhe vlerën në katrorin chi, ka vetëm një gjë të fundit që duhet të bëjmë para se të gjejmë vlerën tonë p-duhet të përcaktojmë nivelin e rëndësisë. Në thelb, niveli i rëndësisë është një matje se sa të sigurtë jemi për rezultatet tona - një nivel i ulët i rëndësisë korrespondon me një probabilitet të ulët që rezultati i një eksperimenti të jetë për shkak të rastësisë dhe anasjelltas. Niveli i rëndësisë shkruhet si një numër dhjetor (p.sh. 0.01), që korrespondon me përqindjen e shansit që rezultati i eksperimentit ishte për shkak të rastësisë (në këtë rast, 1%).
- Sipas konventës, shkencëtarët zakonisht vendosin një vlerë të rëndësishme për eksperimentet e tyre në 0.05 ose 5 përqind. Kjo do të thotë që rezultatet eksperimentale që korrespondojnë me këtë nivel rëndësie kanë, më së shumti, një shans 5% të rastësisë. Me fjalë të tjera, ekziston një shans 95% që rezultatet të jenë për shkak të manipulimit të shkencëtarit me ndryshoret eksperimentale, dhe jo rastësisë. Për shumicën e eksperimenteve, besimi 95% në lidhje me marrëdhënien midis dy variablave, konsiderohet të ketë qenë i suksesshëm në demonstrimin e marrëdhënies midis të dyve.
- Shembull: Për shembullin e makinës sonë të kuqe dhe blu, le të ndjekim marrëveshjen shkencore dhe të përcaktojmë nivelin tonë të rëndësisë së 0, 05.
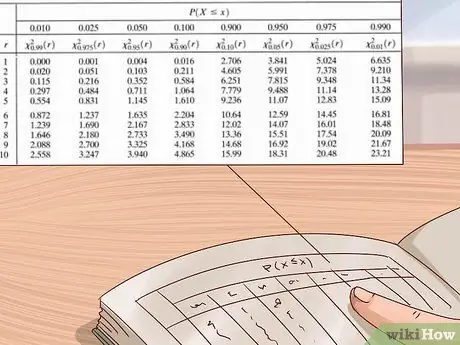
Hapi 6. Përdorni tabelën e shpërndarjes së katrorit chi për të vlerësuar vlerën tuaj p
Shkencëtarët dhe statistikuesit përdorin tabela të mëdha vlerash për të llogaritur vlerat p për eksperimentet e tyre. Kjo tabelë zakonisht shkruhet me boshtin vertikal në të majtë që tregon shkallët e lirisë dhe boshtin horizontal në krye që tregon vlerat p. Përdoreni këtë tabelë duke gjetur fillimisht shkallët tuaja të lirisë, pastaj duke lexuar rreshtat nga e majta në të djathtë derisa të gjeni vlerën e parë që është më e madhe se vlera juaj në katrorin chi. Shikoni vlerën p në krye të kolonës-vlera juaj p është midis kësaj vlere dhe vlerës tjetër më të madhe (vlera e djathtë është në të majtë të saj).
- Tabelat e shpërndarjes Chi square janë të disponueshme nga një sërë burimesh - ato mund të gjenden lehtësisht në internet ose në tekstet e shkencës ose statistikës. Nëse nuk e keni një, përdorni tabelën e treguar në foton e mësipërme ose një tabelë falas online, siç është ajo e dhënë nga medcalc.org këtu.
-
Shembull: Katrori ynë chi është 3. Pra, le të përdorim tabelën e shpërndarjes së katrorit chi në foton e mësipërme për të gjetur një vlerë p të përafërt. Meqenëse ne e dimë se eksperimenti ynë ka vetëm
Hapi 1. shkallët e lirisë, ne do të fillojmë nga tabela e lartë. Ne shkojmë nga e majta në të djathtë në këtë rresht derisa të gjejmë një vlerë më të lartë se
Hapi 3. - vlera jonë në katrorin chi. Vlera e parë që gjejmë është 3.84. Duke kërkuar këtë kolonë, ne shohim se vlera përkatëse e p është 0.05. Kjo do të thotë që vlera jonë p është midis 0.05 dhe 0.1 (vlera tjetër më e madhe p në tabelë).

Hapi 7. Vendosni nëse do të refuzoni ose mbroni hipotezën tuaj zero
Meqenëse keni gjetur një vlerë p të përafërt për eksperimentin tuaj, ju mund të vendosni nëse do të refuzoni apo jo hipotezën zero të eksperimentit tuaj (si kujtesë, kjo është hipoteza që variabla eksperimentale që keni manipuluar nuk kishte asnjë efekt në rezultatet që keni vëzhguar). Nëse vlera juaj p është më e ulët se vlera juaj e rëndësisë, urime-ju keni vërtetuar se ekziston një probabilitet i lartë që të ketë një lidhje midis variablave që keni manipuluar dhe vëzhgimeve tuaja. Nëse vlera juaj p është më e madhe se vlera juaj e rëndësisë, nuk mund të thoni me siguri se rezultatet që po vëzhgoni janë rezultat i rastësisë së thjeshtë ose manipulimit të eksperimentit tuaj.
- Shembull: vlera jonë p është midis 0.05 dhe 0.1. Kjo do të thotë, nuk është aspak më e vogël se 0.05, kështu që, për fat të keq, ne nuk mund të hedhë poshtë hipotezën tonë zeroMe Kjo do të thotë që ne nuk arrijmë kufirin minimal të besimit prej 95% që kemi vendosur në mënyrë që të thuhet se policia në qytetin tonë u jep bileta biletash makinave të kuqe dhe blu në një raport që është krejt i ndryshëm nga mesatarja kombëtare.
- Me fjalë të tjera, ekziston një shans 5-10% që vëzhgimet tona nuk janë rezultat i një ndryshimi në vendndodhje (duke analizuar qytetin tonë, dhe jo të gjithë pjesën), por janë rastësi. Meqenëse ne po kërkojmë një probabilitet më të vogël se 5%, nuk mund të themi se ne i bindur që policia në qytetin tonë tenton të marrë bileta për makina të kuqe - ekziston një mundësi e vogël por statistikisht shumë e ndryshme që ata të mos kenë këtë tendencë.
Këshilla
- Një kalkulator shkencor do t'i bëjë llogaritjet shumë më të lehta. Ju gjithashtu mund të kërkoni për llogaritës në internet.
- Ju mund të llogaritni vlerat p duke përdorur disa programe kompjuterike, duke përfshirë softuerin e përdorur zakonisht dhe një softuer statistikor më të specializuar.






